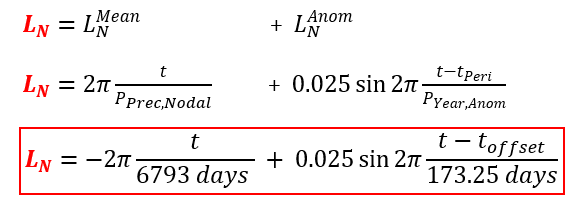Solar Eclipse Prediction (Complex Version)
By Spencer Connor
Note: if you are just learning about the geometry of eclipses I’d suggesting starting with: Eclipse Prediction (Simple) to understand the concepts first. This article will be using terms which are not common knowledge, I will be doing my best to define or link to descriptions to help.
The three big questions
Solar eclipse prediction really boils down to three components:
When will there be a solar eclipse?
This is the bulk of the work, figuring out the orbital geometry needed to produce an eclipse and tracking each component until they occur in the right combination of ranges.
What kind of eclipse will it be?
The is likely the easiest as well as the least impactful for getting wrong, but it remains a necessary task.
Where will the eclipse occur on Earth?
This ultimately is derived from #1, but with the added consideration of the earth’s axial tilt and its relatively rapid rotation.
We’ll be tackling these questions in that order.
When will there be an eclipse?
Lunar Variables
We know from our understanding of the geometry of eclipses that their are a finite number of variables that must known to predict eclipse occuring. Those for the moon are:
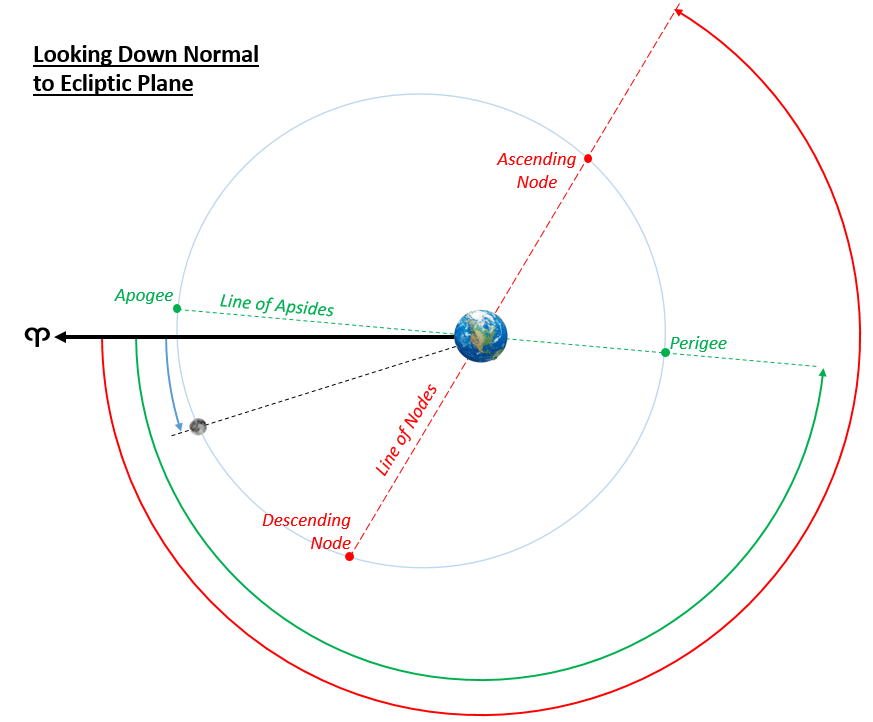
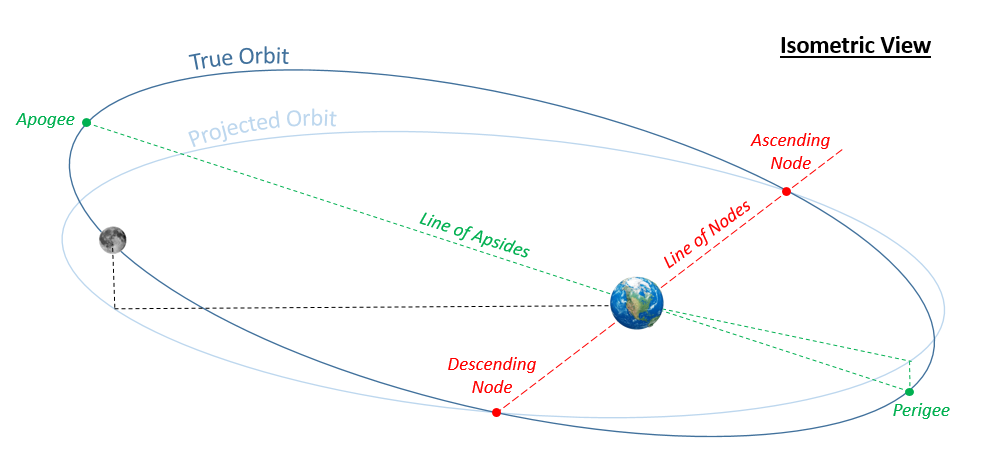
The position of the moon along either the lunar orbit or along the ecliptic. For ease, I’ll be using the ecliptic and more specifically the ecliptic longitude of the moon, which is the angle from a fixed reference (here the first point of Aries, ♈︎) and the moon’s projection from its plane to the ecliptic. Note that this is different from the modern term of True Anomaly, which is referenced from perigee.
The position of the lunar nodes, since these are at the intersection of the lunar orbit and the ecliptic either could be used without projection correction. I’ll used the ecliptic and again reference from the first point of Aries and to the ascending node, creating the ecliptic longitude of the ascending node. In this instance it is synonymous with the more modern term Right Ascension of the Ascending Node (RAAN) but I’ll use longitude for consistency.
The position of lunar perigee, in this case we will project it from the lunar orbit to the ecliptic and reference it from the first point of Aries as well to make the ecliptic longitude of perigee. Note this is not the modern usage of the argument of perigee (AoP) which is referenced from the ascending node instead.
Solar Variables
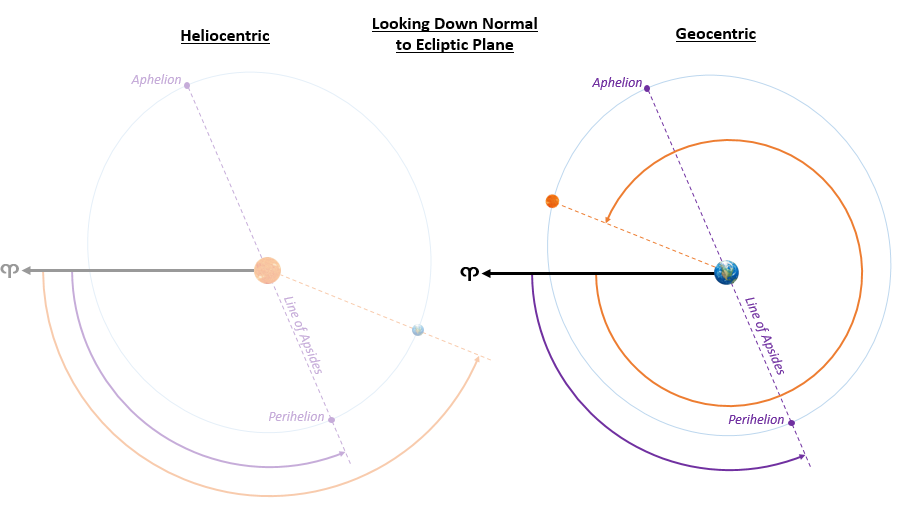
There are also two variables to track for the sun. Note that this is best done in a geocentric frame (although I show heliocentric as well for reference). They end up being essentially the same except for a 180° flip when referencing sun-from-earth rather than earth-from-sun. Note that we make no claims of forces behind the motion of these celestial bodies here, so the issue of geocentric being “incorrect” is not applicable. It’s only when one claims that the geocentric frame is inertial that physics breaks. I’ll continue to use the geocentric convention for these angles for the remainder of the page.
The position of the sun along the ecliptic. Again, this will be referenced from the first point of Aries (♈︎) and is thus the ecliptic longitude of the sun.
The location of perihelion of the sun, with the same reference of the first point of Aries this creates the ecliptic longitude of perihelion.
Ecliptic Longitude of Perihelion
We’re going in order of easiest to most complex and the ecliptic longitude of perihelion is certainly the place to start because it can be considered a constant for most applications. Technically the earth’s line of apsides precesses, but it has a period of about 112,000 years and a small enough influence on the solar longitude that 1000 years of precession still only results in about 15% of a solar diameter error (0.07 deg). This term will get captured as an offset in the ecliptic longitude of the sun instead, and will be compensated for there.
Ecliptic Longitude of the Sun
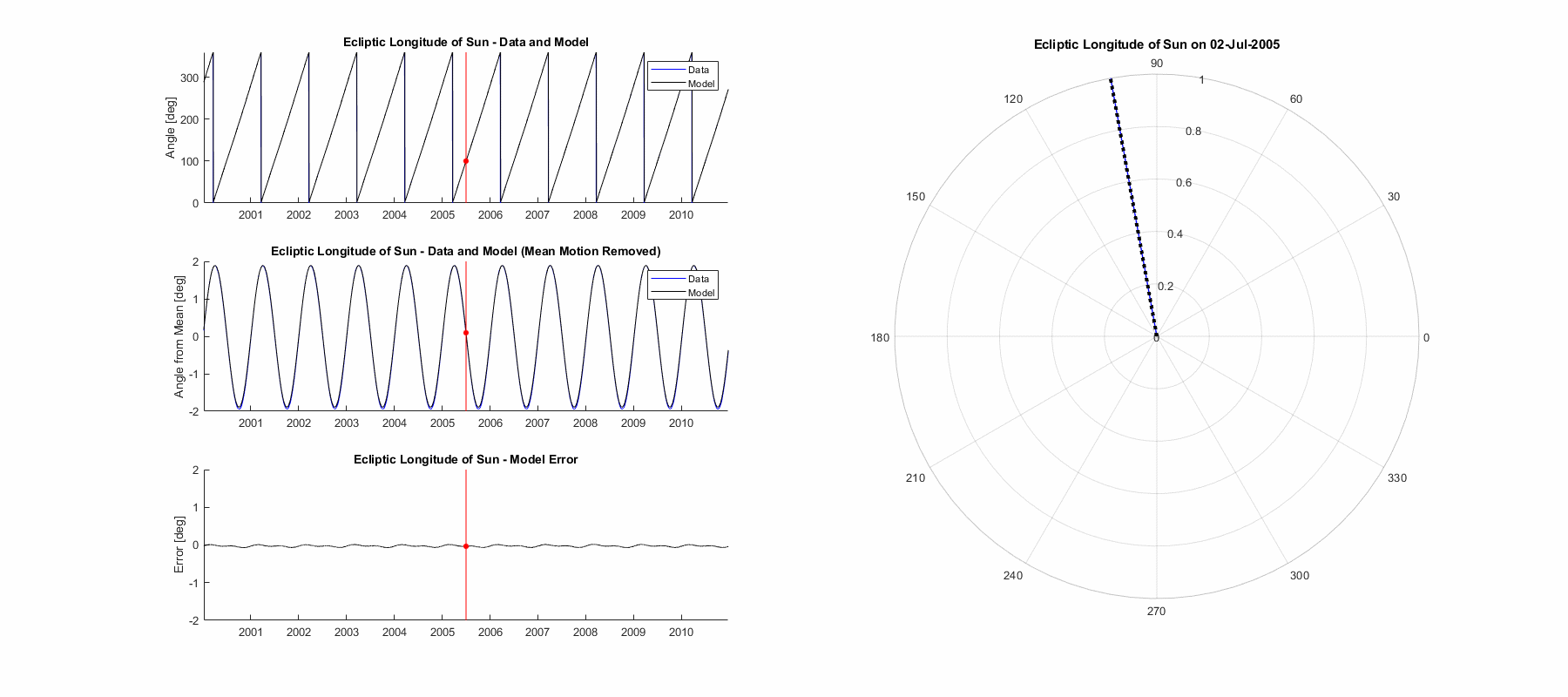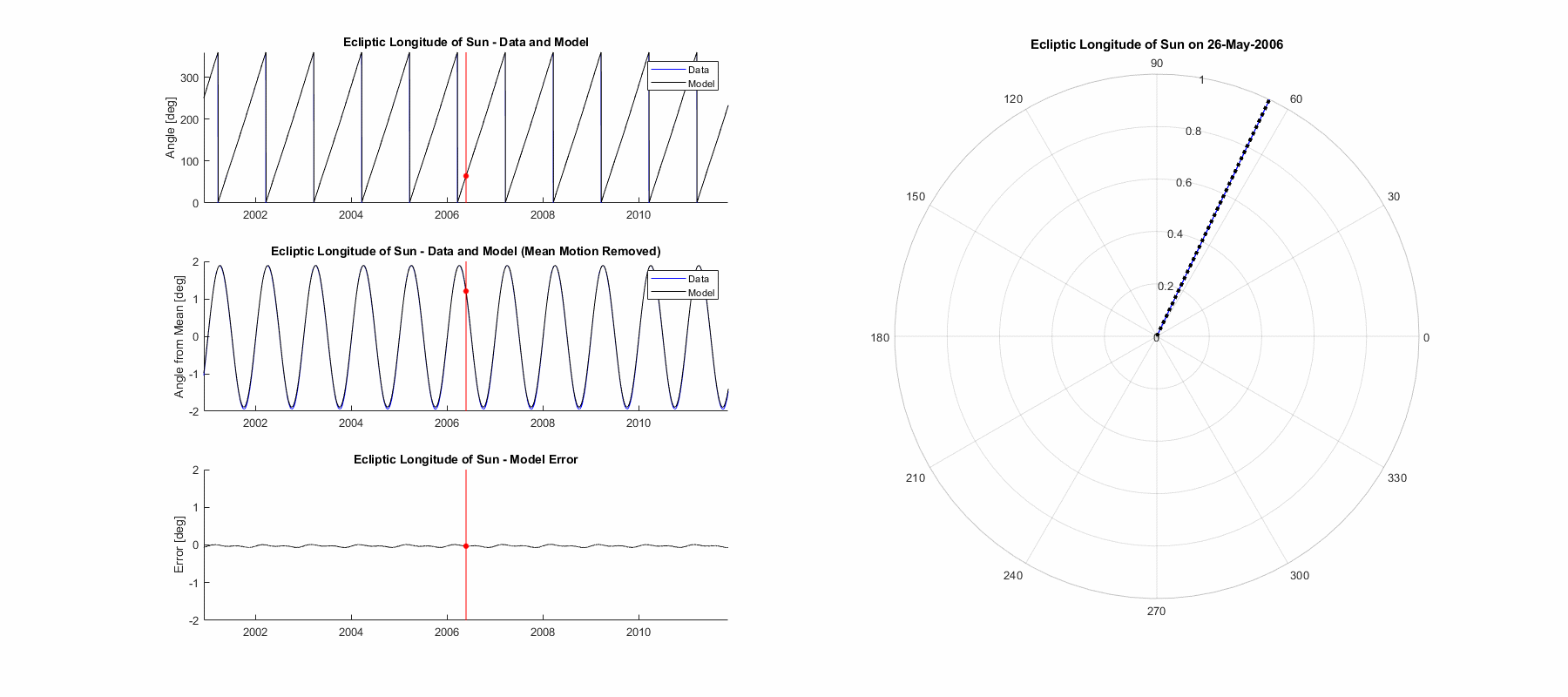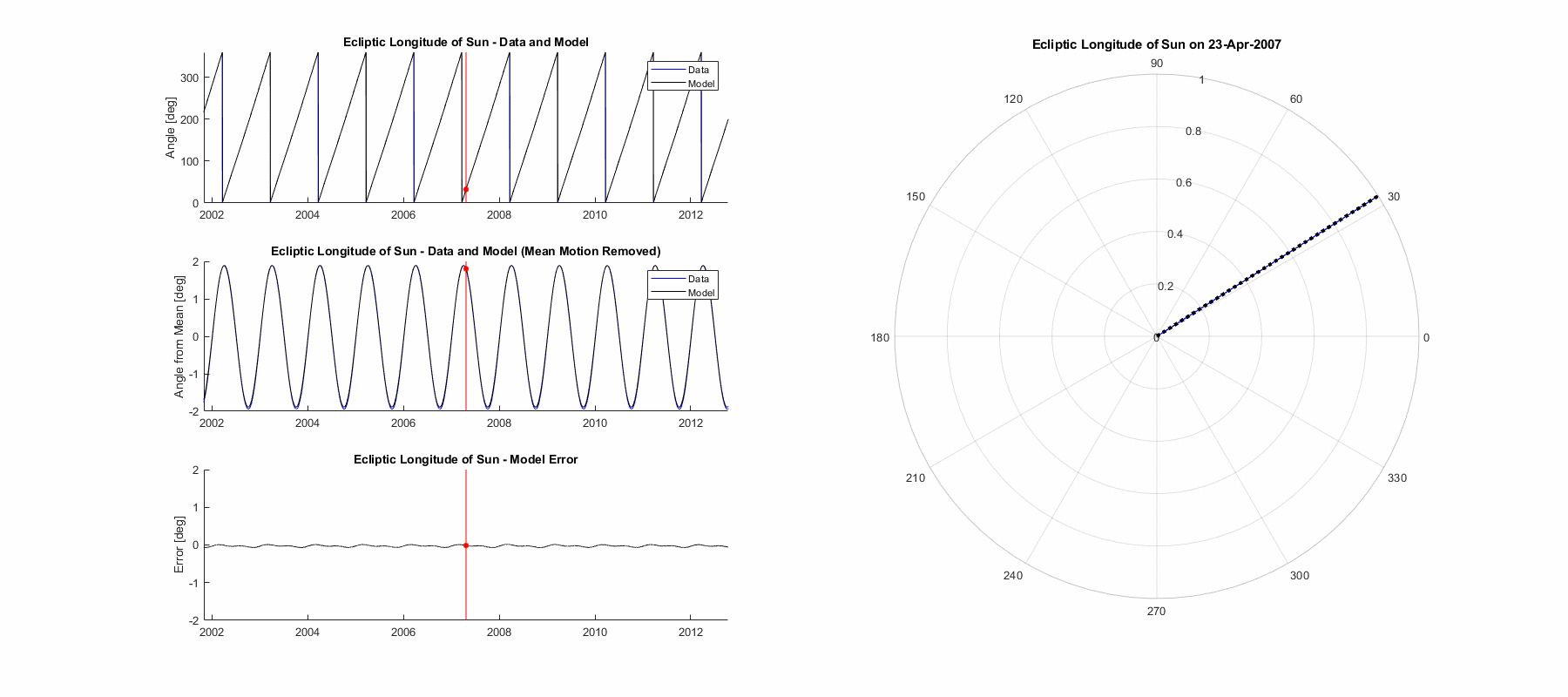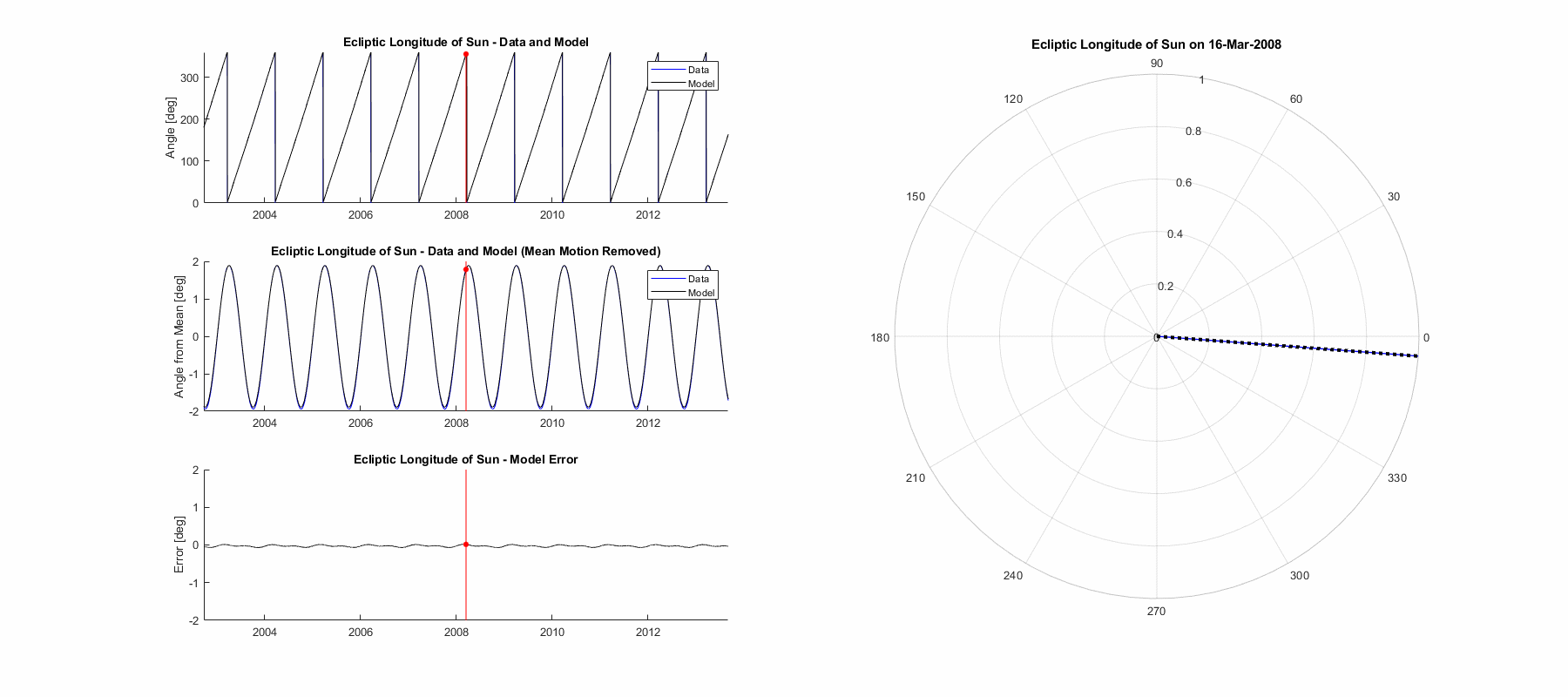
Unfortunately the ecliptic longitude of perihelion is the only term we could largely ignore, but the ecliptic longitude of the sun is one of the simplest and illustrates the method used for the others. All of the terms have a mean motion and are generally rotating in a single direction, just with uneven motion. The first step is to determine that mean motion, for the ecliptic longitude of the sun it take one year for the sun to go around and return to the same celestial direction (or in reality for the earth to), so the mean motion is one sidereal year (365.2564 days). In the first graph below we can see what looks like a sawtooth to this effect, the angle is steadily increasing and then rolls over at 360° to 0°. The next graph down subtracts out that ramping mean motion and reveals an oscillation that was layered on it.
This is the Equation of the Center resulting from Kepler’s Equation, showing the angle increasing faster (i.e. the body moving faster) at periapsis. A direct result of Earth’s orbital eccentricity, we can determine the magnitude of the variation from that value (shown on right). We’re only considering the first order term since the effect of the subsequent ones is so small. This oscillation was originally called the Solar Anomaly, here we can use a sine function to approximate it pretty well. The final equation for the ecliptic longitude of the sun is shown on the right, including the mean motion and the anomaly added to it. Notice also that the solar anomaly term uses an anomalistic year, which is slightly different from the sidereal year. It is different by precisely the apsidal precession rate of 112,000 years for a full rotation mentioned for the ecliptic longitude of perihelion term. This is how that effect is captured as the phase of this anomaly term goes VERY slowly out of phase. The accuracy of the resultant modelling function is excellent, as we should hope for for the simpler terms. Mean error is 0.029°, max error is 0.071°, and 3σ (99.7%) error is 0.066°.
Ecliptic Longitude of the Ascending Node
The ecliptic longitude of the ascending node uses the exact same approach as the ecliptic longitude of the sun with a mean motion and a single sinusoidal oscillation over it. The causes of both are different however, the mean motion comes from the nodal precession of the moon’s orbit (which is mainly a solar gravity interaction) and occurs over about 18.6 years and in a retrograde (westward) direction. The oscillation has a period of 173.25 days, which is the time between the sun aligning with successive nodes and therefore eclipse seasons. The magnitude of the oscillation has no mathematical derivation from first principles and ends up around 1.4° or 0.025 rad, interestingly enough large enough to entirely halt the mean motion temporarily. The equation has the same form as before, just with different variables. The accuracy of the resultant modelling function is not quite as good, as to be expected from a more turbulent gravitational environment. Mean error is 0.178°, max error is 0.898°, and 3σ (99.7%) error is 0.680°.
Ecliptic Longitude of Perigee
The ecliptic longitude of perigee uses the exact same approach as the previous but has two notable frequencies oscillating over the mean motion instead of one. The first has a period of 31.8 days and a magnitude of 15.4° (0.270 radians), the second a period of 205.9 days and a magnitude of 9.57° (0.167 radians). Note that these are significant perturbations, perigee is by far the most chaotic of the terms and the modelling and resulting accuracy reflect that. Thankfully ecliptic longitude of perigee is only used to characterize the eclipse rather than determine it, so the functional consequence of its inaccuracy (annular vs total vs hybrid type is off) is less drastic than location being off and missing the event. Mean error is 2.9°, max error is 15.3°, and 3σ (99.7%) error is 11.5°.
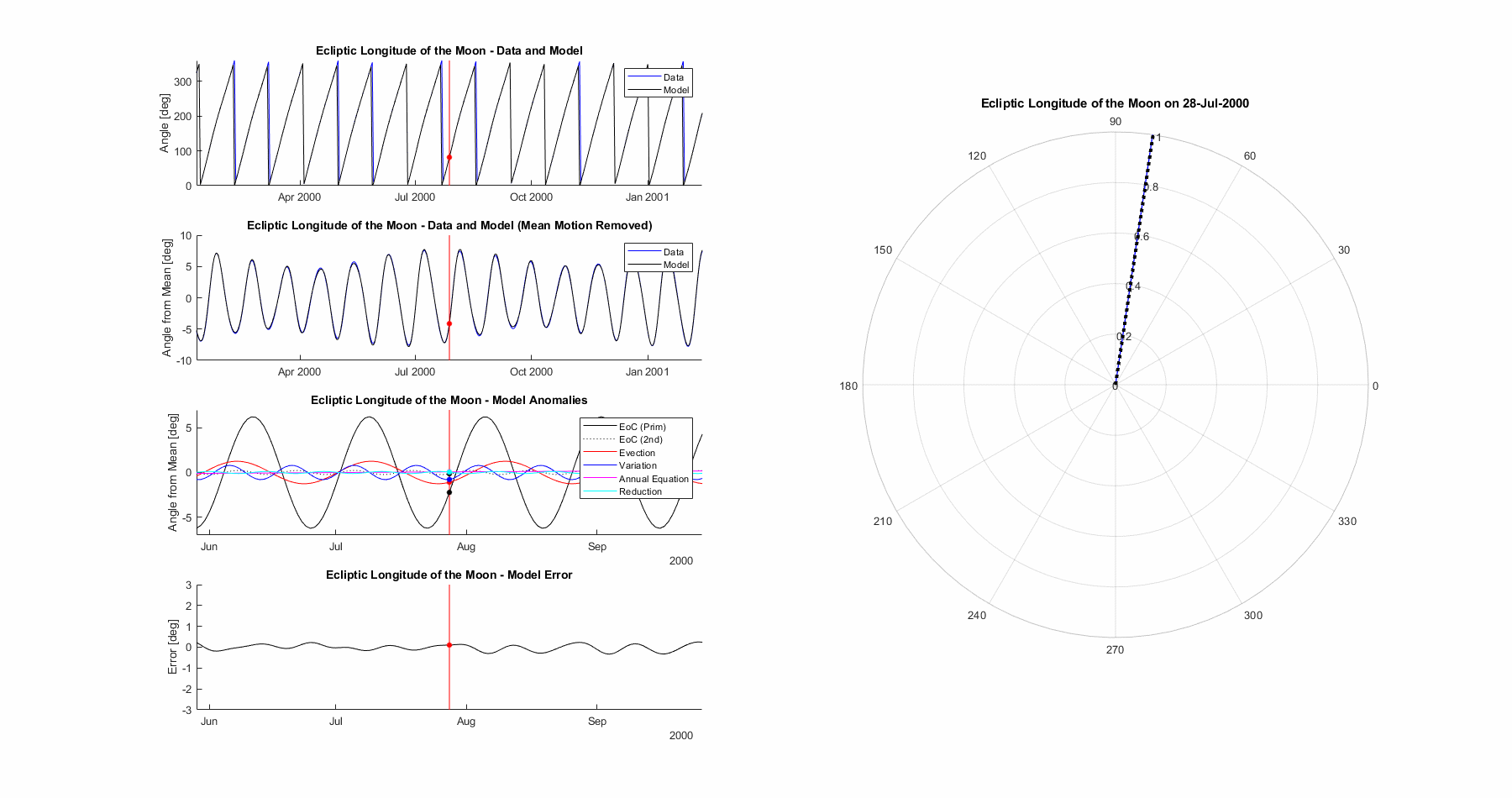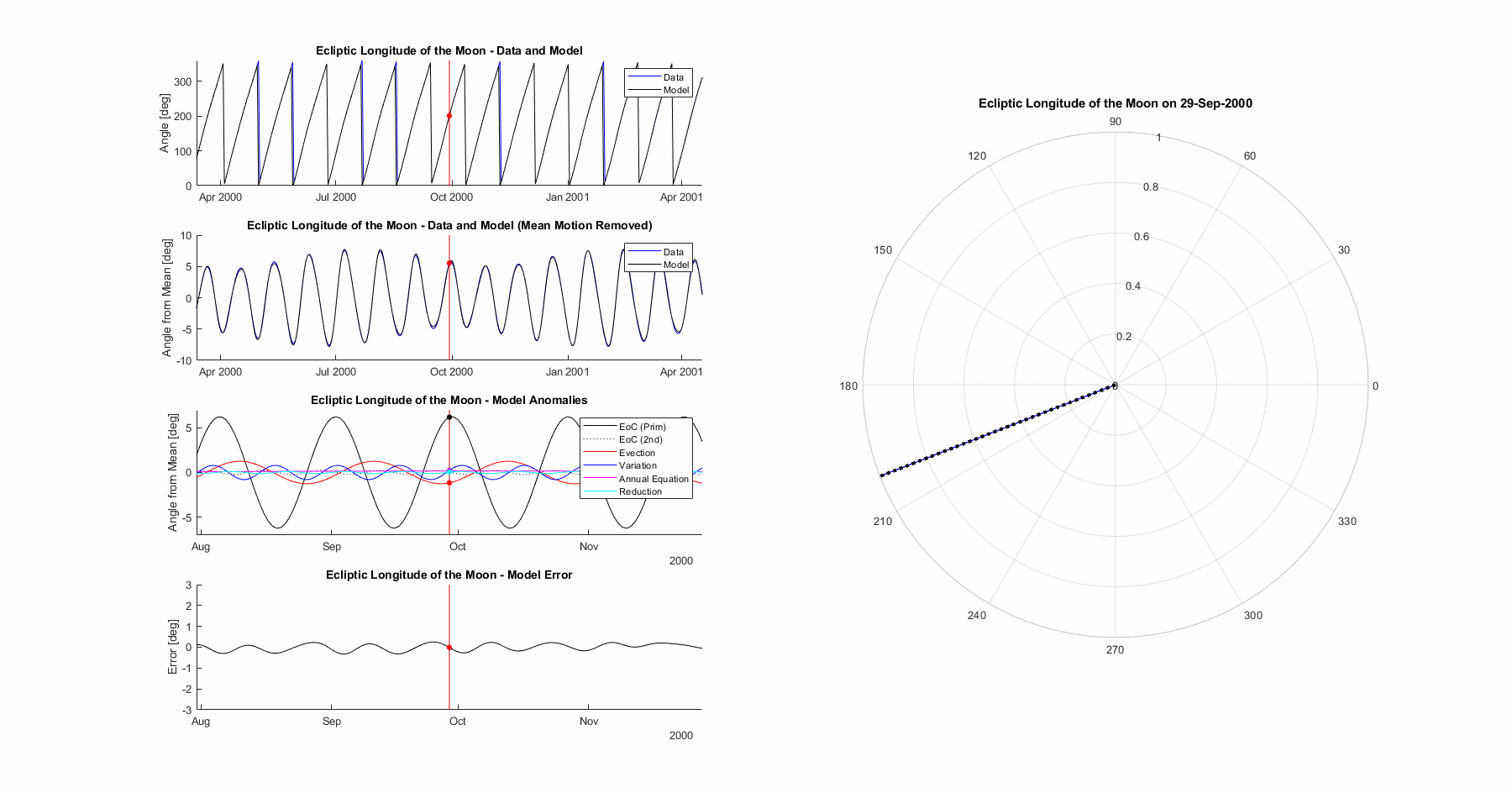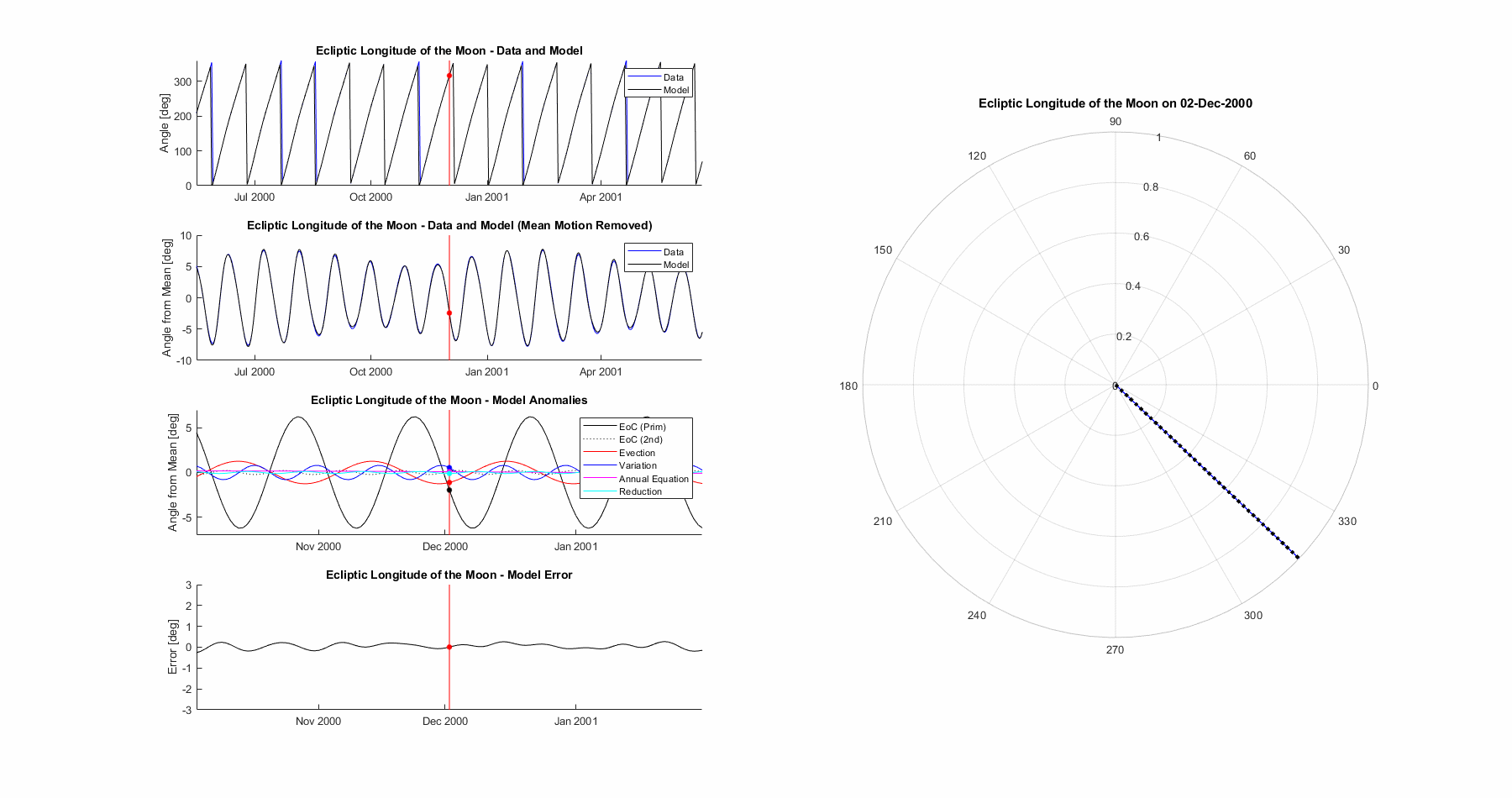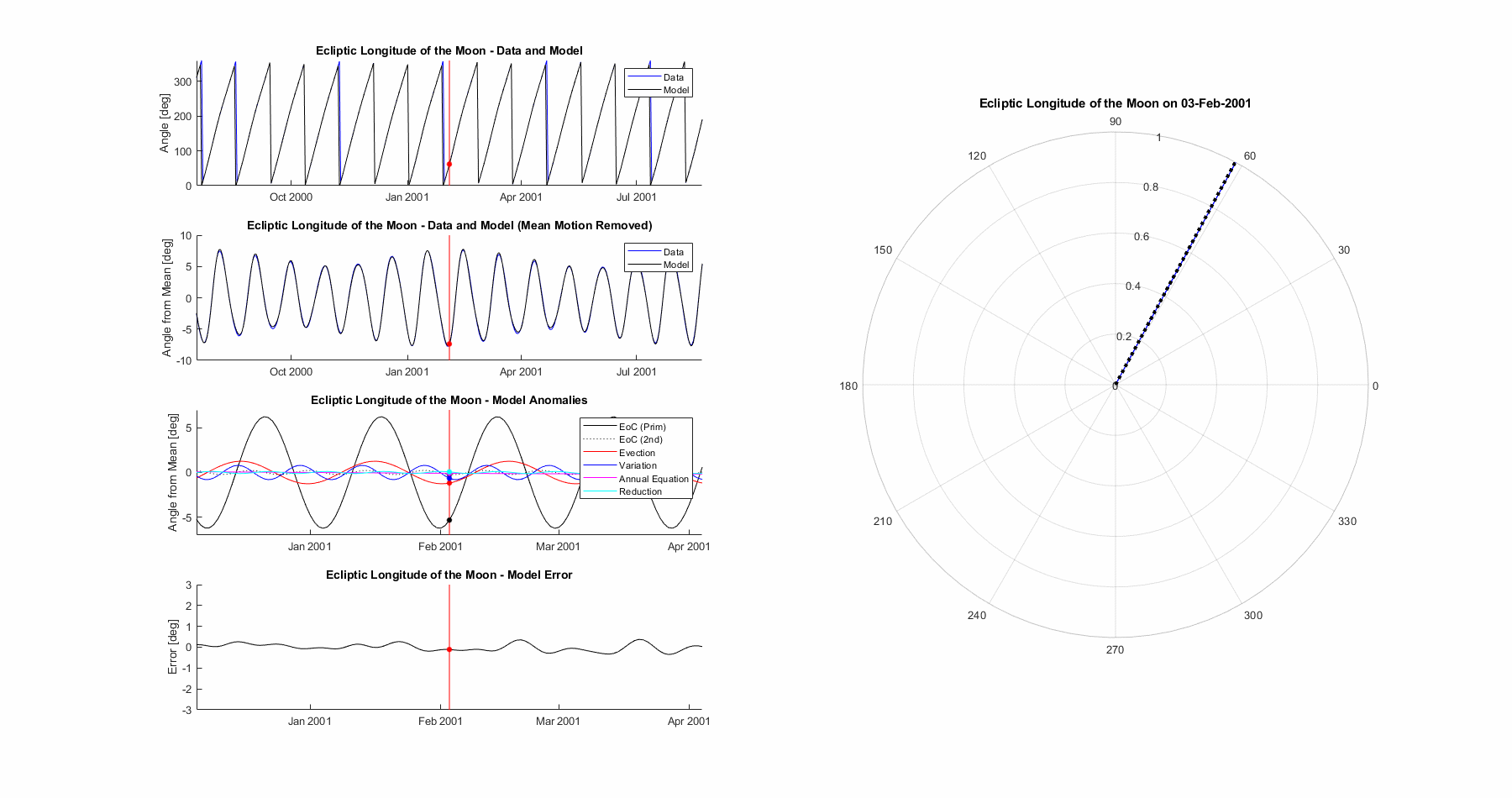
Ecliptic Longitude of the Moon
The ecliptic longitude of the moon is the big bad one, the joyous combination of both critical to get right as well as complex to model. While previous terms had mean motion and one or two anomalies in addition, we’ll need a minimum of 5 anomalies (modelled with 6 sine functions) in addition to the mean motion to get anywhere close.
Let’s run through them here:
Mean Motion. Period of one sidereal lunar month (27.322 days)
Equation of the Center / Great Anomaly. Primary period of one anomalistic lunar month (27.554 days) although the effect is significant and non-sinusoidal enough that it is appropriate to include a second order approximation at half the period. Primary period amplitude of 6.24° (0.109 rad) and secondary period amplitude of 0.229° (0.004 rad).
Evection. Period of 31.8 days and a magnitude of 1.261°. A rather odd period that comes from the sun’s gravitational influence on the eccentricity of the moon’s orbit.
Variation. Period of half a synodic month (14.77 days) and a magnitude of 0.802°. Another solar perturbation, this one seeing the moon accelerate slightly when new and full and slow at the quarters.
Annual Equation. Period of one anomalistic year (365.2596 days) and a magnitude of 0.172°. This comes from the varying influence of the sun based on the earth-sun distance.
Reduction. Period of half a draconitic month (13.61 days) and a magnitude of 0.115°. Reduction is the result of projecting the moon’s position from its orbit to the ecliptic
The resultant model is seen below. Mean error is 0.132°, max error is 0.522°, and 3σ (99.7%) error is 0.486°.
What Type of Solar Eclipse will it Be?
The type of solar eclipse is entirely determined from the relative sizes of the sun and moon:
If the sun is larger than the moon (earth near perihelion, moon near apogee) the result is an annular eclipse
If the sun is smaller than the moon (earth near aphelion, moon near perigee) the result is a total eclipse
There is also a transitional case called a hybrid eclipse, where along the path of totality which celestial body appears larger changes. Note that this is primarily due to the lunar distance changing (both as a result of the lunar eccentricity and from the radius of the earth causing those at the subsolar point to be closer than elsewhere).
Both sun and moon apparent sizes can be approximated with sine waves as shown below, with periods of an anomalistic year and anomalistic month.
Where Will the Eclipse be Visible?
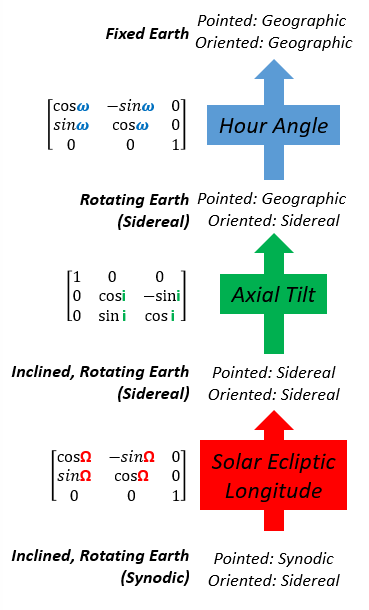
For this next piece we need to understand that the the occurrence of the eclipse occurs relative to the subsolar point. A perfect sun-moon-earth syzygy would cause an eclipse directly on this point, but invariable the eclipse path passes north of this (if the moon is slightly above the ecliptic at minimum solar elongation) or south (if the moon is slightly below the ecliptic at minimum solar elongation). The eclipse path always begins on the west side of the earth and progresses generally eastward but can head north-east or south-east depending on the time of year and which node. The geometry for this is extensive, though not necessarily obscure. Ultimately we need to formulate what the earth looks like from the viewpoint of the sun, and how the moon transits across in that frame. That first part can be done with a discrete series of coordinate transforms that take between a fixed earth frame (for which we can use latitude and longitude coordinates) and a frame pointed along the sun-earth vector. Then we back-track through the coordinate frames to return to geographic coordinates.
Putting it all together
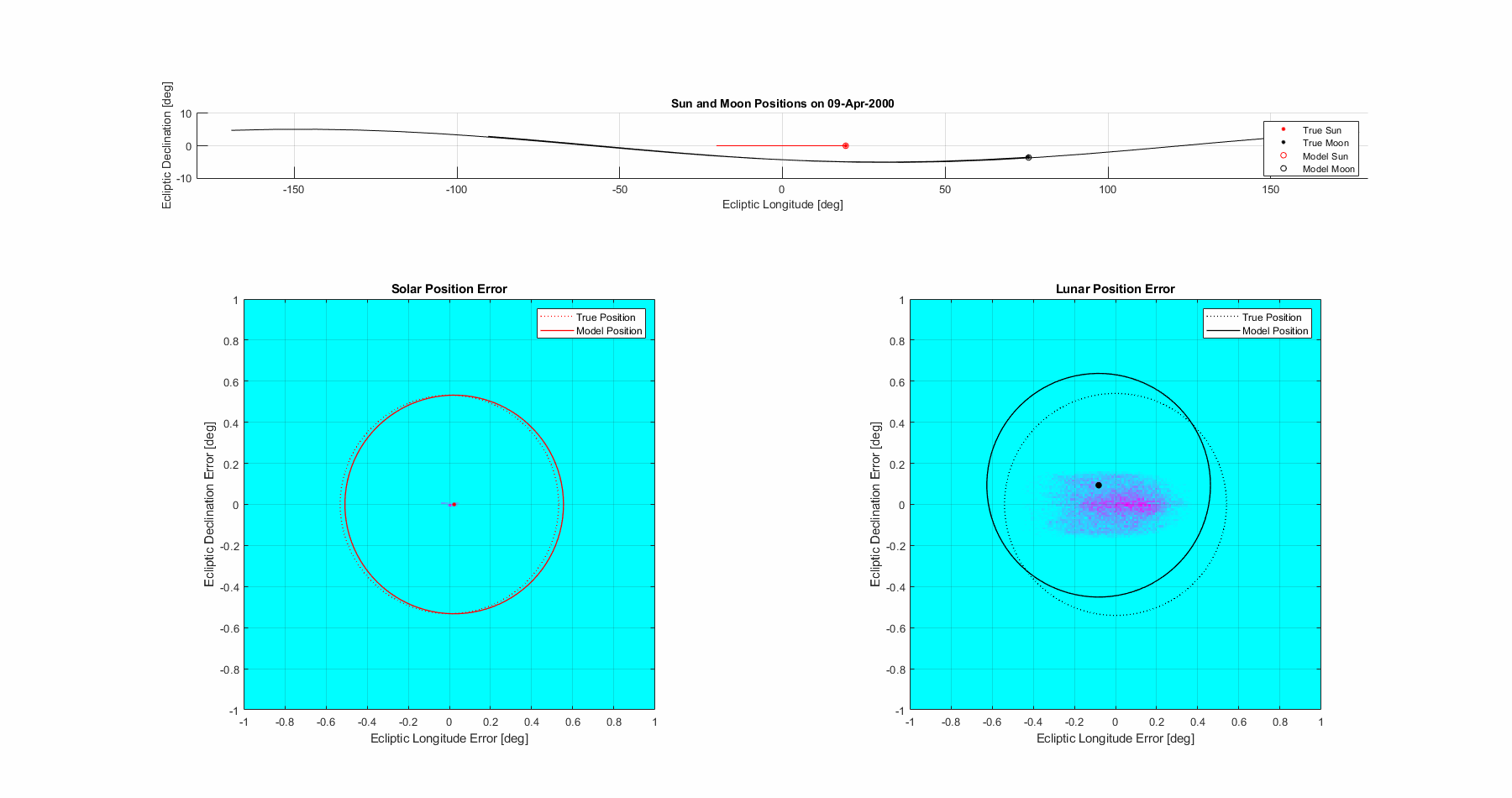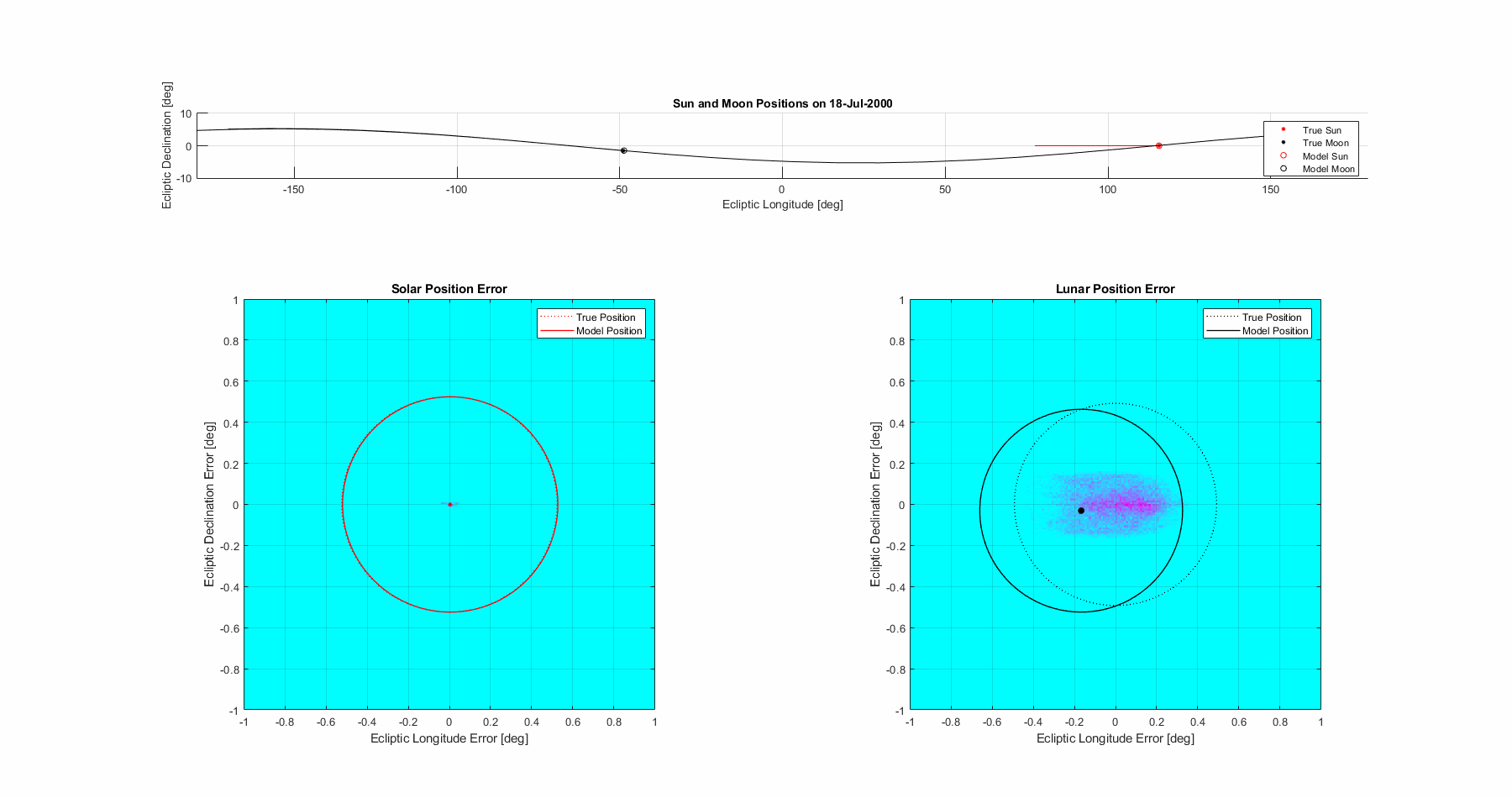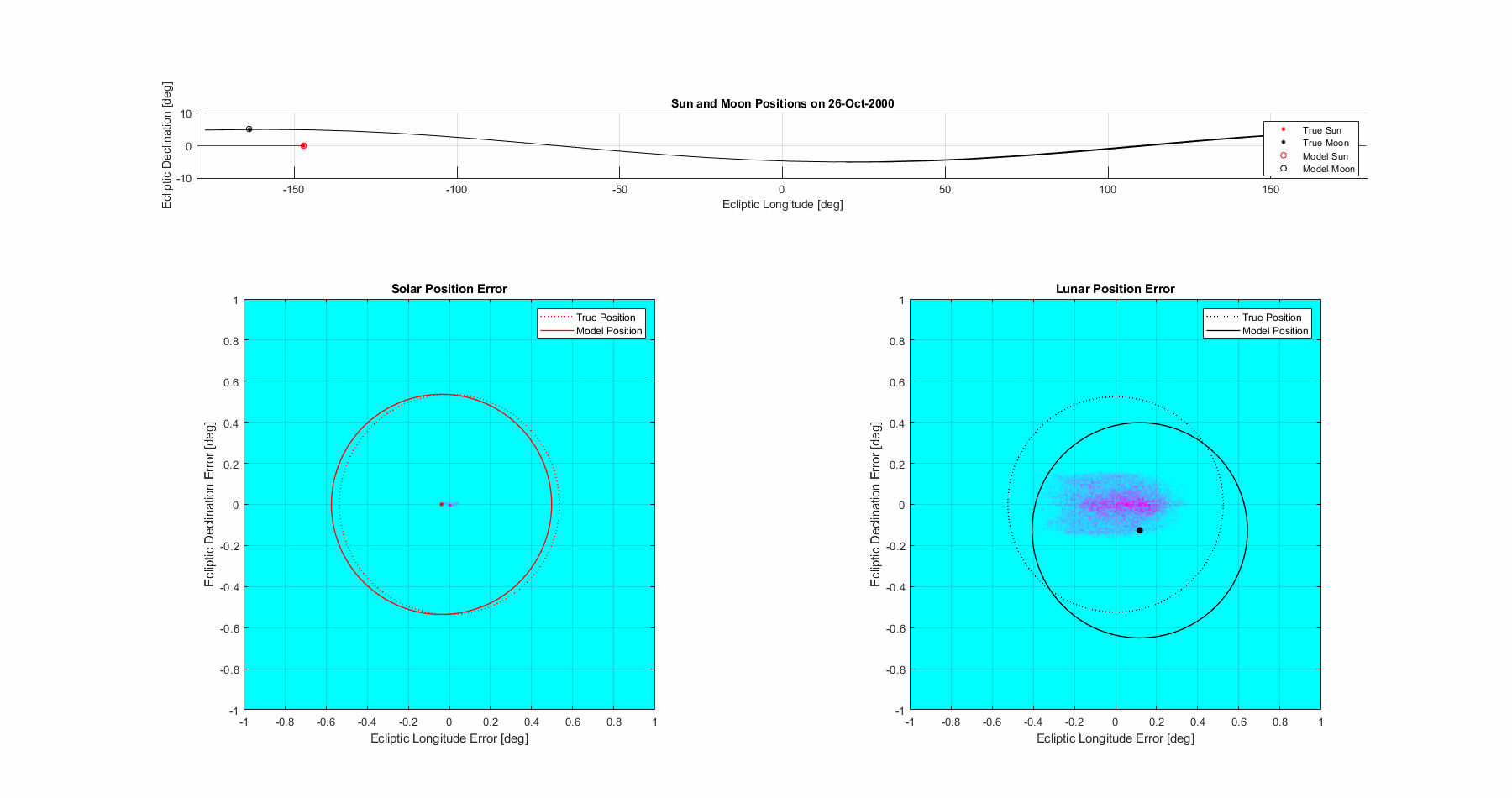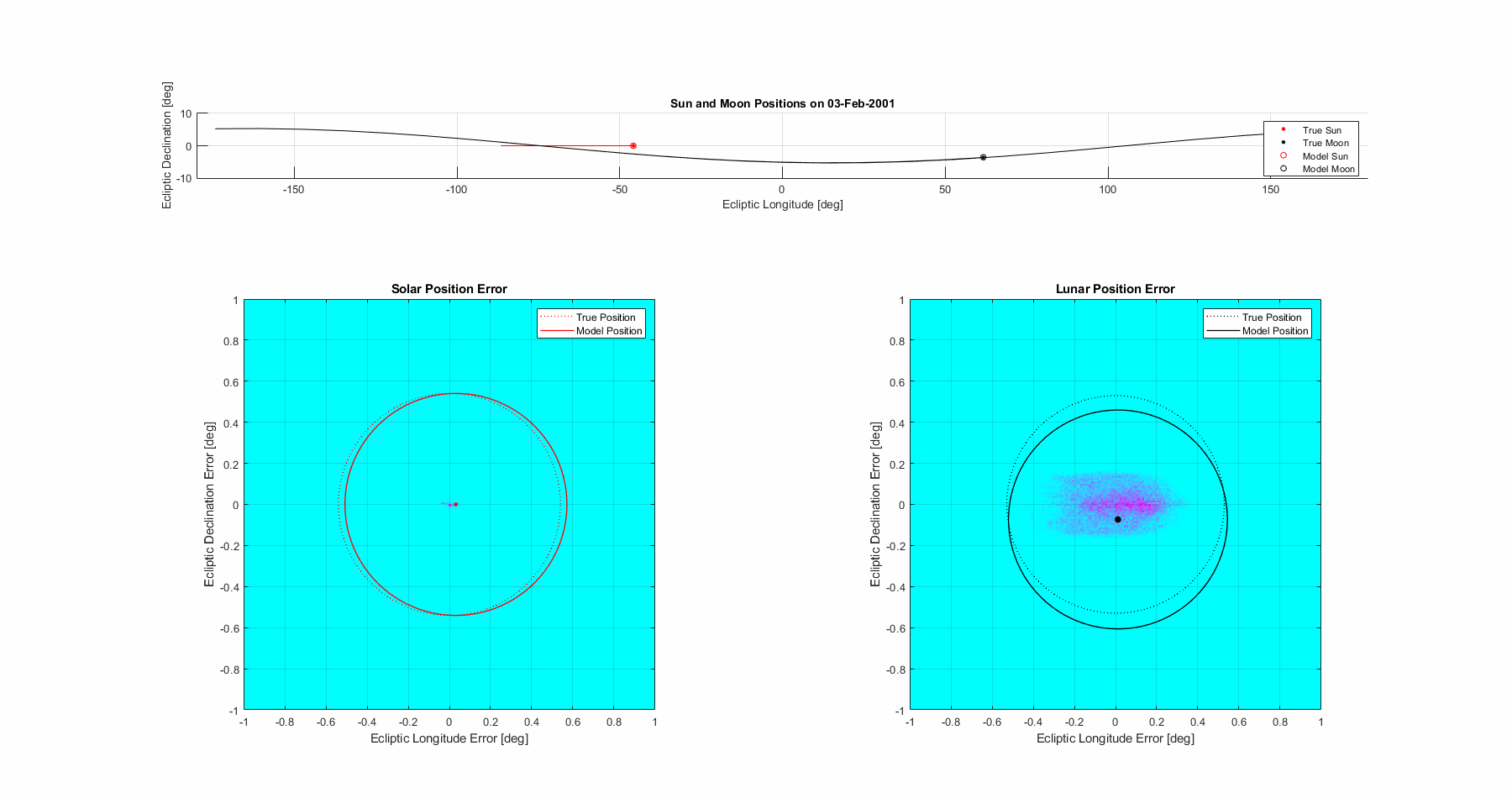
With the required parameters all defined mathematically, let’s take a look at how accurate it is in a few different ways. Let’s start with with just simply determining the position of the sun and moon as seen from an centralized earth observer. We’ll use a fixed mean inclination of the moon’s orbit of 5.14°, in reality it does have a libration but functionally since the influence on position when the moon is at a node goes to zero it isn’t a major source of inaccuracy for eclipses. It’s pretty clear that the sun has minor error in the longitudinal direction, but primarily the moon is showing visibly chaotic motion. Recall that this is after about a 20x reduction through the 5 lunar anomalies, illustrating the complexity of the motion.
But that alone doesn’t tell us what the error in terms of predicting timing and location on the earth, so let’s wrap all of this up into an aggregate simulation and run a few known eclipses.
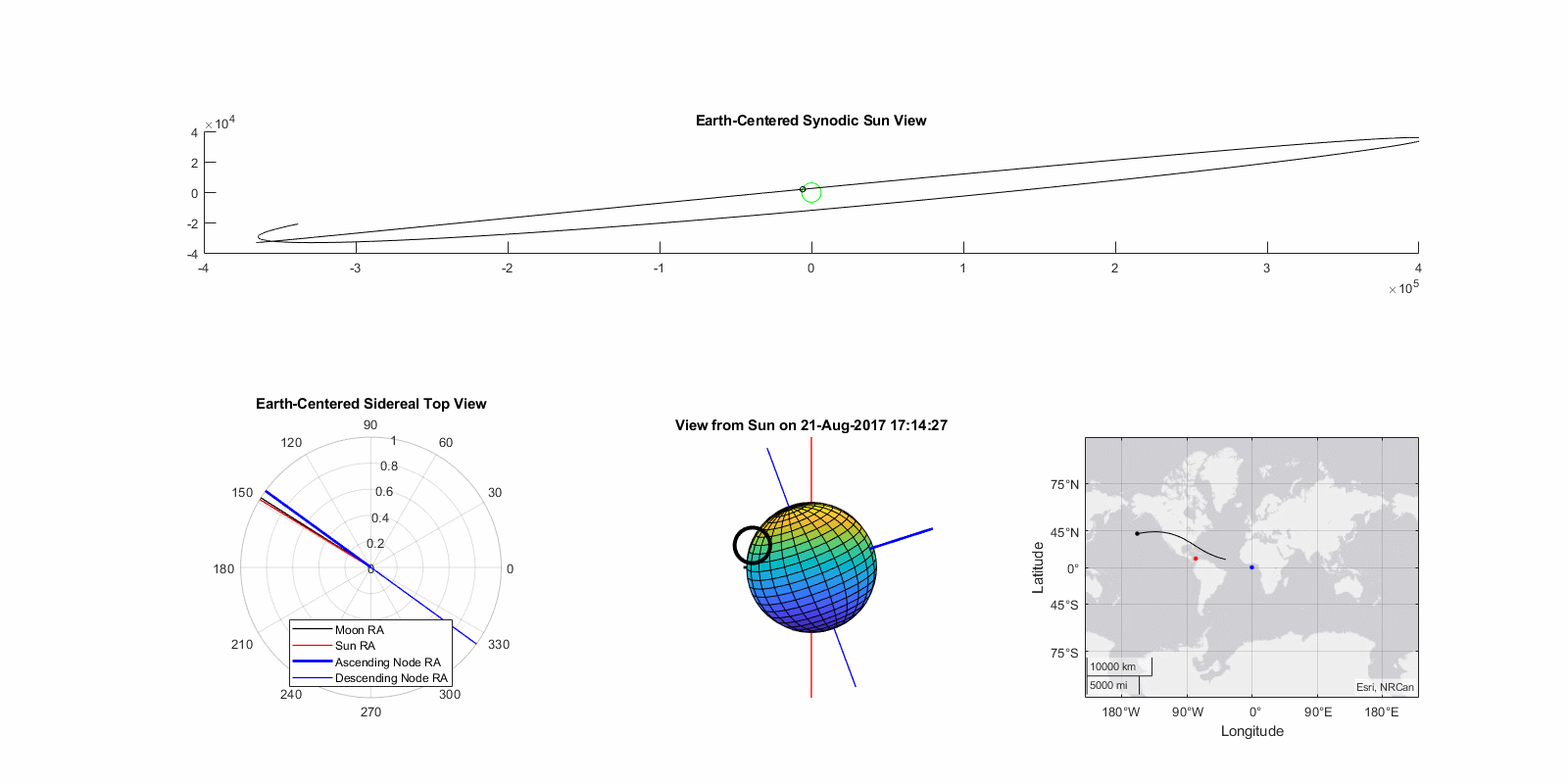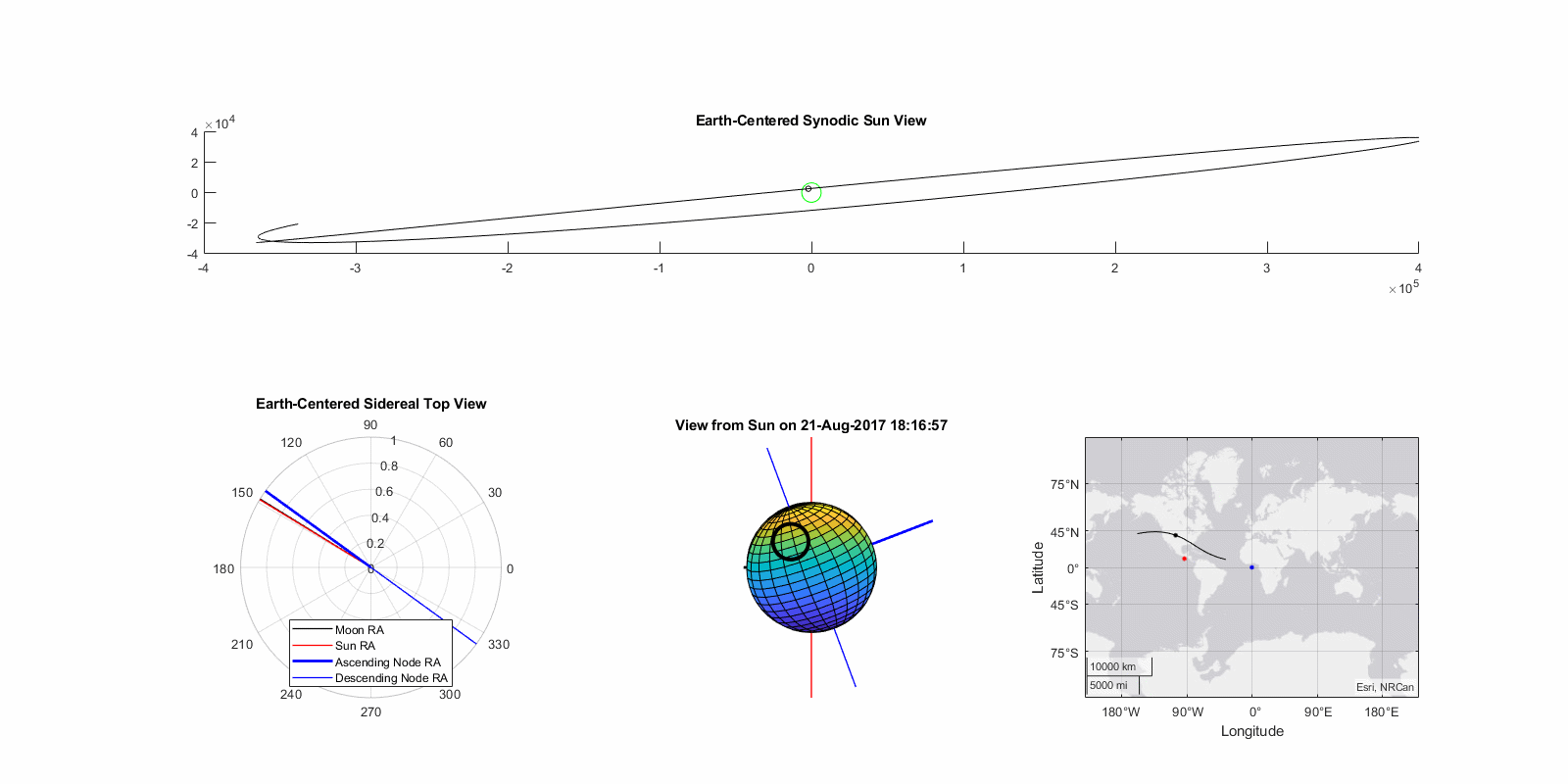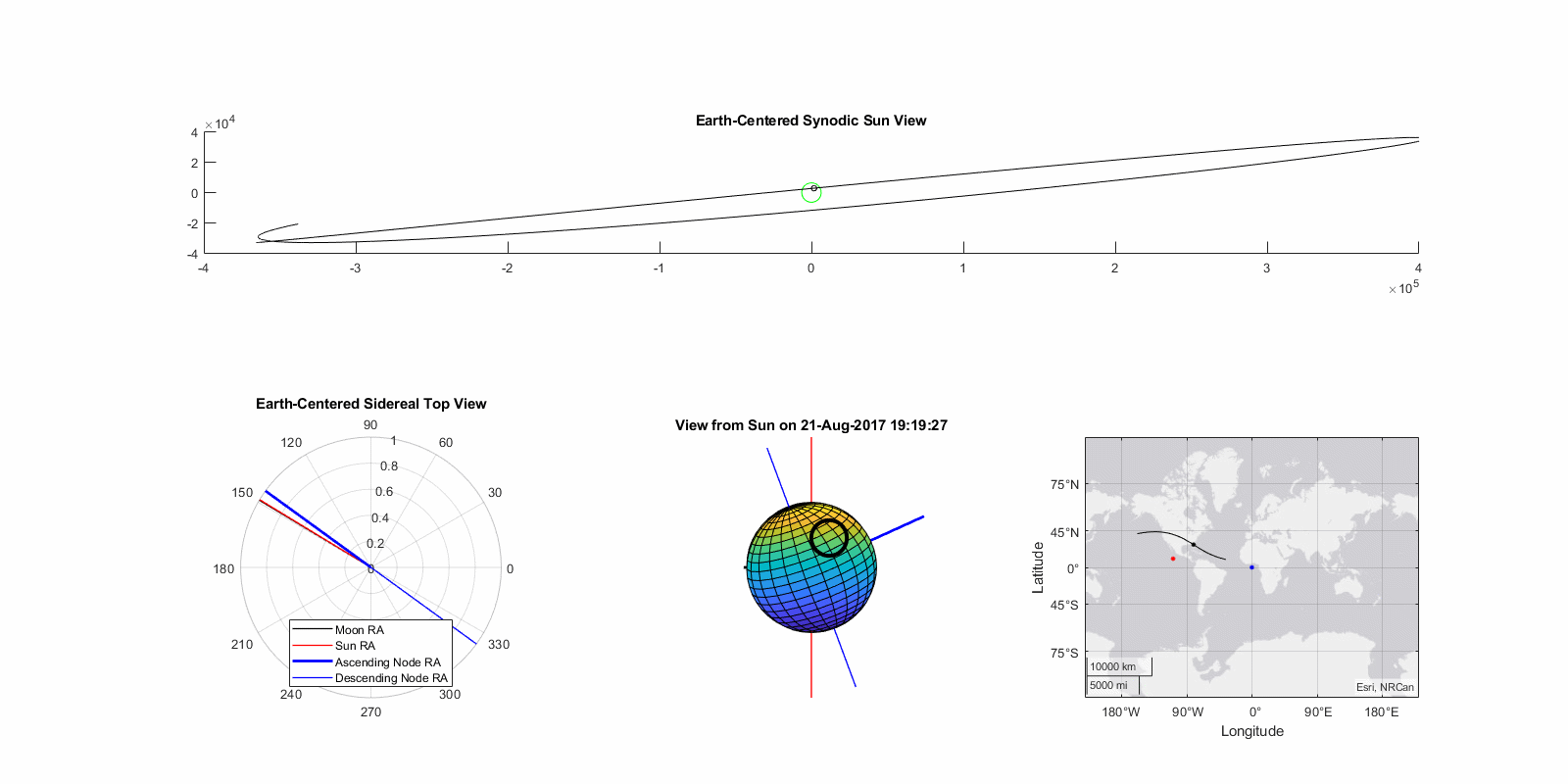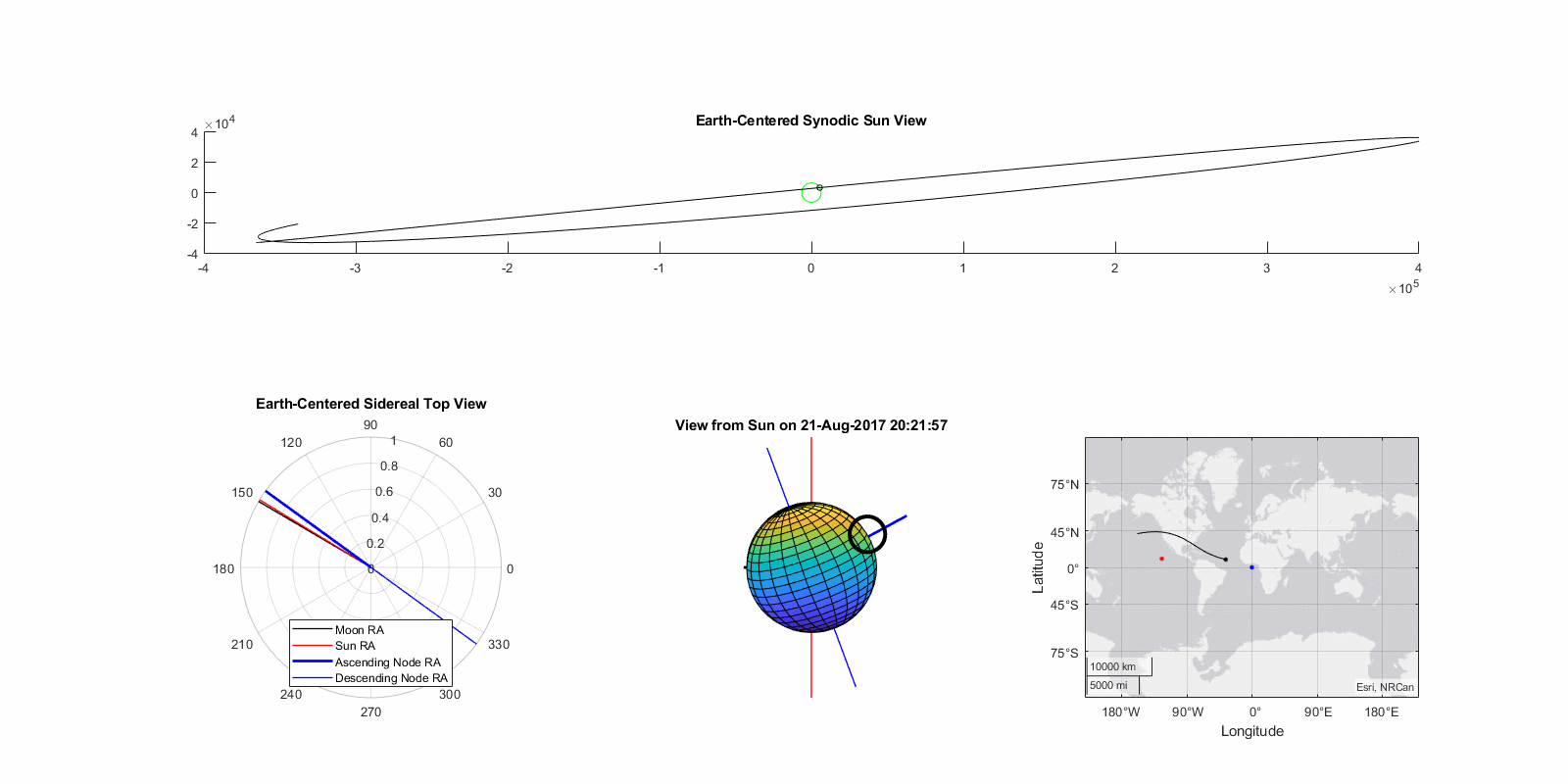
Eclipse of Aug 21th, 2017 (Great American Eclipse)
The so-called “Great American Eclipse” was an ascending node total eclipse whose totality path crossed the contiguous United States for the first time in almost a century. Occurring close to the fall equinox and a few days after lunar perigee, the magnitude was 1.03. The model predicted a magnitude of 1.01, an error of -2.5%. True gamma was 0.437 and the model predicted 0.424, an error of -2.9%. The eclipse paths are shown on right, the maximum path error was approximate 70 nautical miles or about twice the width of totality. Functionally, this means that while this model will predict the occurrence, timing, type, and approximate location of the eclipse it is not sufficiently accurate to position an observer in the path of totality reliably.
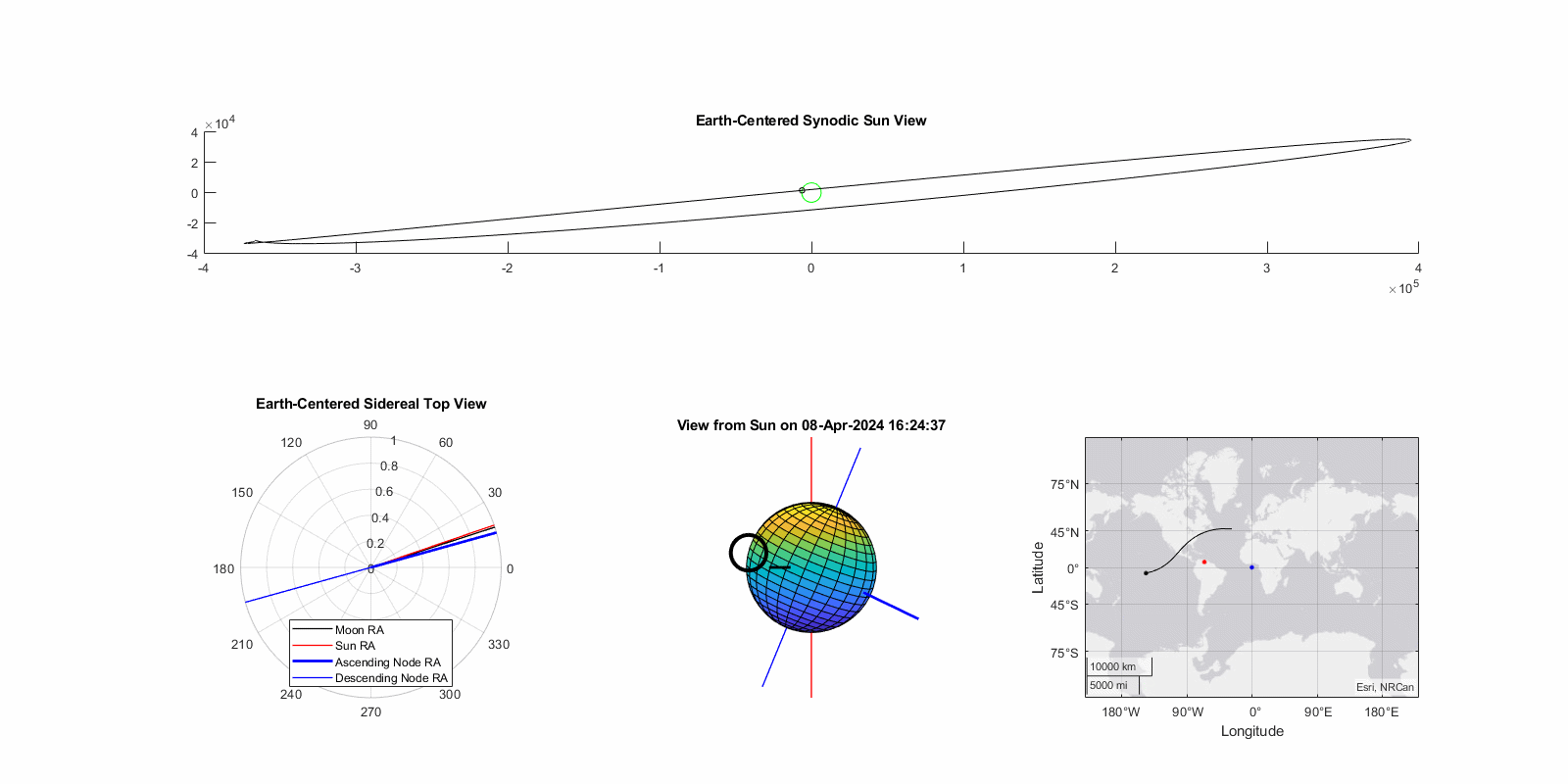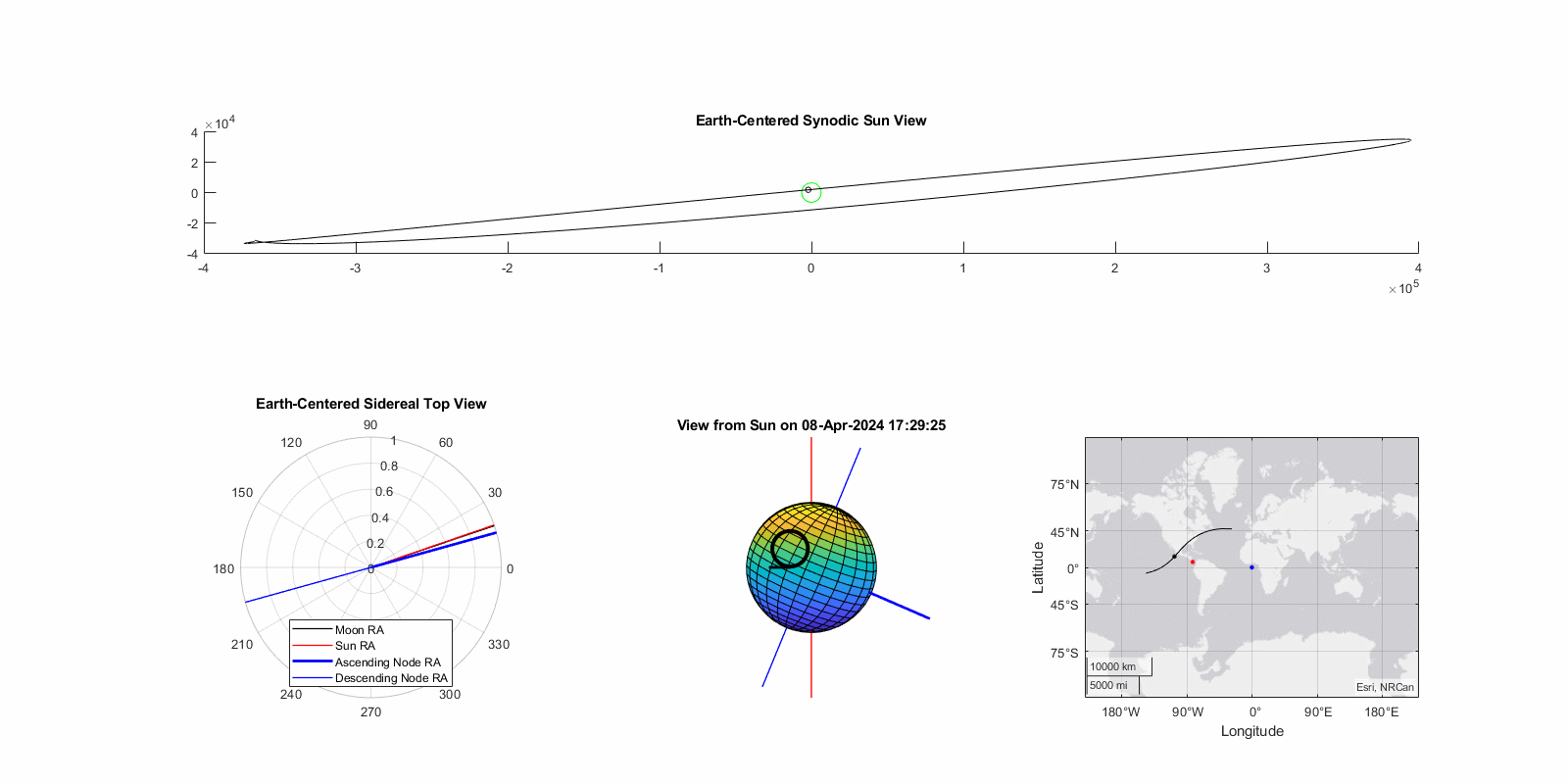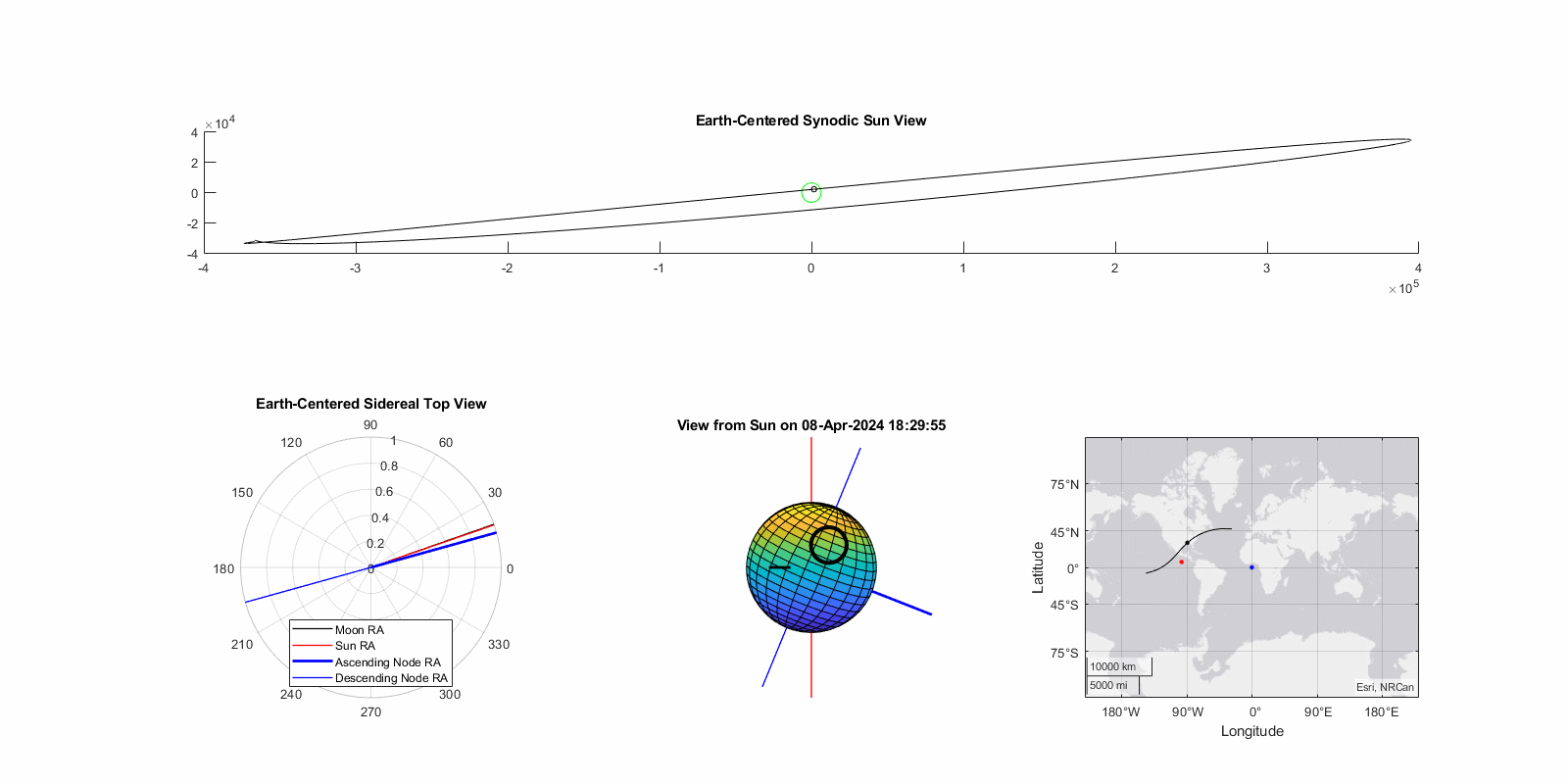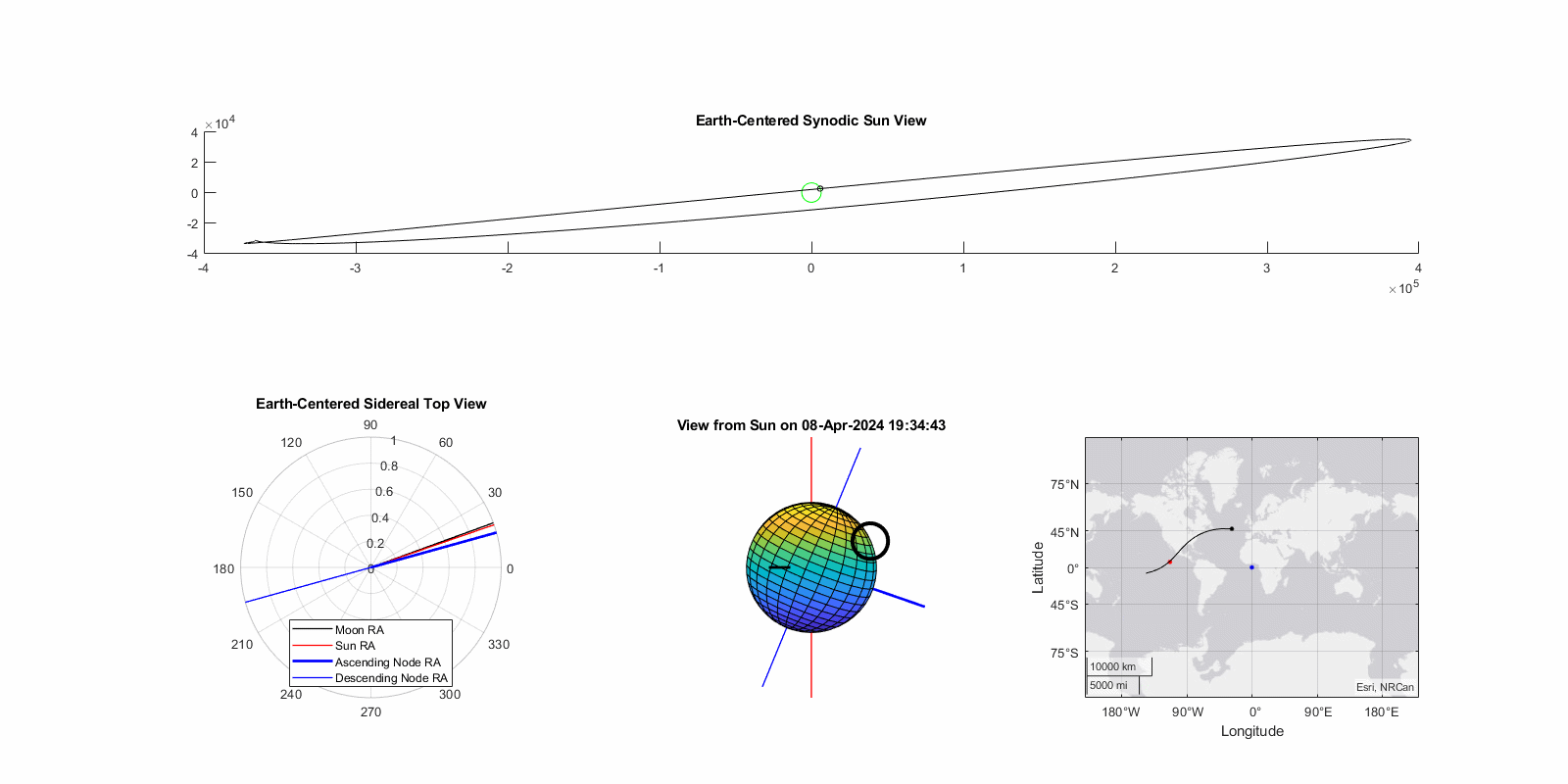
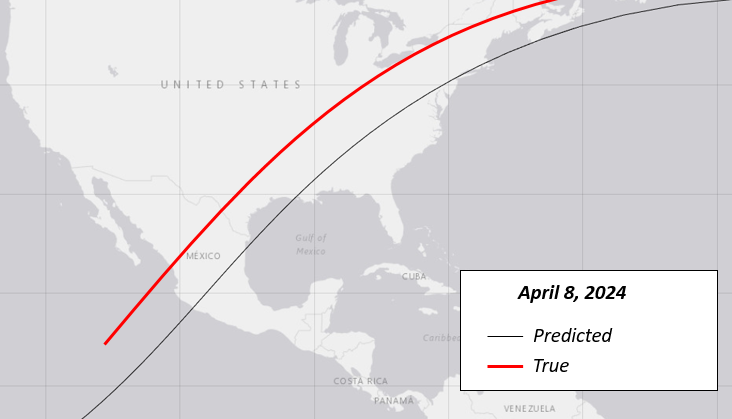
Eclipse of April 8th, 2024 (Great North American Eclipse)
Dubbed the “Great North American Eclipse”, this was also an ascending node total eclipse that primarily crossed the United States. Note that due to it occurring near the vernal (spring) equinox rather than the fall equinox the path of totality progresses south-to-north instead. While ascending node vs. descending node difference effects this angle by ~5° it is dwarfed by the seasonal effect of ~23° from the Earth’s axial tilt. This eclipse occured only a day after lunar perigee, thus the magnitude is relatively high at 1.06. The model predicted 1.02, a -3.6% error. True gamma was 0.34 and the model predicted 0.32, a -7.9% error. The geographic error is larger as seen on right, approximately 100 nautical miles. Again, insufficient to pre-position an observer for totality.