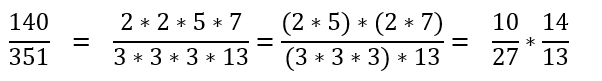Stern-Brocot Tree and Gearing
Why to Use a Stern-Brocot Tree
One topic you may see pop up quite a bit related to determining gear ratios is the Stern-Brocot tree. It is an elegant mathematical structure that helps determine the closest fraction to a given irrational number, such as the target gear ratios derived from planetary motion. A fraction is helpful because it can be exactly created with a gear pair with teeth equal to the numerator and the denominator.
For example, if we need a gear ratio of 1.234 discovering that fraction 21/17 = 1.235 would allow us to use a 21T and 17T gear to get very close to this target!
In the simplest terms, the tree starts from a seed ratio of 1/1, and with each iteration both expands in its range as well as increases its resolution within that range. This is very helpful as the target gear ratio and the accuracy to which we need to match it are generally known very early in the design process.
Figure 1. The Stern-Brocot Tree down to three levels/iterations. Note how each new level both expands the range of fractions as well as decreases the difference between adjacent fractions (higher resolution, and therefore lower error for any nearby target gear ratio).
Accuracy of Stern-Brocot Solutions
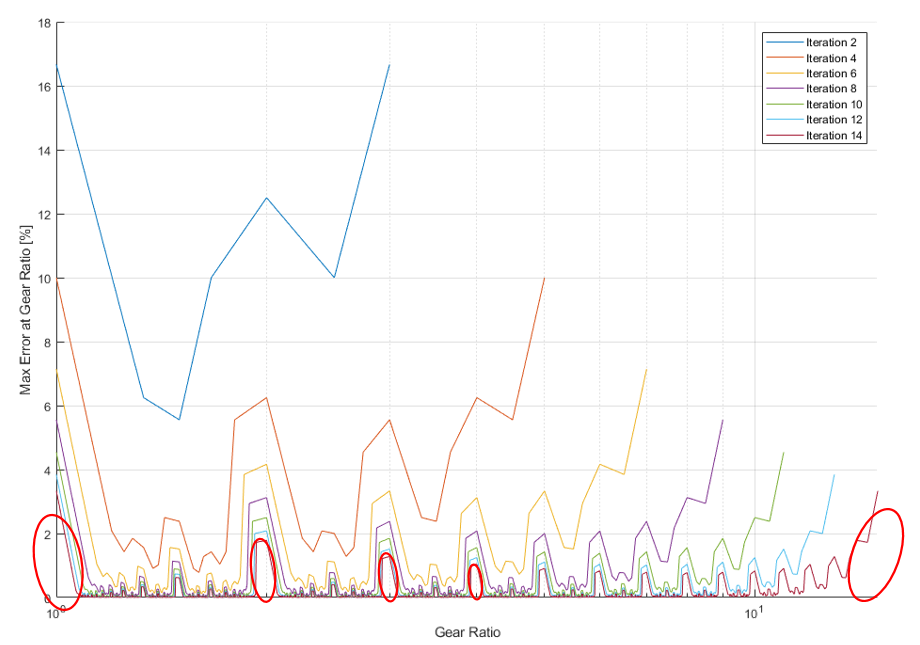
The Stern-Brocot Tree expands non-uniformly at a net 2^N rate, and you can see in Figure 2 that even a 14th order tree (~65,000 elements) still has regions of gear ratios with error well over 1%.
However, there are two important features of the Stern-Brocot tree that make it very powerful to calculate the nearest fraction to extreme resolution:
Each fraction is the mediant of the two above it and therefore is unaffected by the rest of the tree
Each level always remains sorted by magnitude
Together this means that there is no need to calculate a whole tree. One can algorithmically determine which branch to go down and continue iterating a very small subset of the tree until the necessary accuracy is reached. Computational time just dropped from O(2^N) to O(3*N)!
In Figure 3 you can see how many iterations it took for 10,000 randomly generated sets of gear ratios to reach three different target accuracy levels.
Figure 2. Resolution/Error of Stern-Brocot Tree after various iterations. Notice that while the range expands and error reduces with each resolution, error at the extremes and other distinct locations remains relatively high. It’s largely chance whether your desired ratio ends up in these regions or not.
Figure 3. How many iterations it takes to achieve 1%, 0.1%, & 0.01% accuracies for randomly generated gear ratios between 1:1 and 1:10. Notice that there is incredible variation as the required accuracy is tightened. Also notice the peaks (required many iterations to get close) appear to be on simple numbers that occur early in the tree which would be very unexpected. Closer inspection reveals these are actually a pair of peaks straddling the nominal value. While the tree quickly includes the integer value, it takes a long time to return to capture a number adjacent to it.
Why NOT to use Stern-Brocot for Gear Trains
Well that all seems like this would be a good tool for calculating the required gears, so what’s the issue? When you use a Stern-Brocot tree you will discover that for reasonable accuracies you’ll end up with somewhat randomized and large numerator and denominators, let’s look at a couple examples to discover why this could be a problem:
Say we were looking for a two gear sets to represent 0.3989 and 3.14159, both to 0.001% accuracy. You would find the closest fractions are 140/351 and 355/113, all of which are prohibitively large gears. This may be an issue for a single-stage gear set, but we can use a compound gear train to break those down into manageable gears.
Let’s start with the first one, we’ll factor it out and see if we can group the numerator and denominator factors into two groups that all have between 10 and 100 teeth:
Solved! We’ll have a 10T gear mesh to a 27T gear, then a 14T gear to a 13T. (Note you can switch these around however you’d please, e.g. 10:13 and 14:27 with the same result)
Okay, let’s look at our next one…
We are unable to group the factors in the same way. 113 is prime and thus cannot be factored, as a result it is impossible to use this fraction without needing a gear of at least 113 teeth. If we force ourselves to tolerate this we’ll also see that 355 cannot be broken into many factors (not a smooth number). Our only recourse is to either add in additional factors equally to both numerator and denominator (as shown in red below), or if this is not possible be forced to choose a different fraction. This could be either lower accuracy or possibly higher accuracy using a three-stage gear train. We’re left with a non-optimal solution, without knowing how it can be improved.
The Takeaway
Despite being tightly knit into the horological community, I would suggest that the Stern-Brocot tree as it applies to gearing is of primarily historical interest. What begins as a deterministic and efficient algorithm ultimately concludes in the sort of manual guess-and-check methodology that it was designed to surpass. The computational power required to evaluate factorization and number smoothness needed to ensure a feasible gear set quickly eclipses that of ‘brute force’ methods that it competes with. With that said, there is something about utilizing methods of historical clockmakers and designing algorithms of more finesse even if they are less efficient.